Industrial chillers remove heat from liquid via vapor-compression, adsorption refrigeration, or absorption refrigeration cycles. Refrigerants, or working fluids, are the substances used in refrigeration cycles where in most cases they transition from a liquid to a gas and back again. Fluorocarbons, especially chlorofluorocarbons, became commonplace refrigerants in the 20th century, but are now being phased out because of their ozone depletion effects. Other common refrigerants are ammonia, sulfur dioxide, and non-halogenated hydrocarbons such as propane.
Ideal refrigerant properties
The ideal refrigerant would be non-toxic, non-flammable, non-explosive, non-corrosive, not harmful to the environment, cheap and easy to produce and work with and have good thermodynamic properties operating at low pressures. The desired thermodynamic properties are a boiling point somewhat below the target temperature and a high latent heat of vaporization to move more heat per volume when it boils. Ideally, the refrigerant should have moderate density in liquid form, a relatively high density in gaseous form, and evaporate and condenses at temperatures easily manipulated with compression. Since boiling point and gas density are affected by pressure, refrigerants may be made more suitable for a particular application by appropriate choice of operating pressures. Lastly, refrigerants should mix well with oil, so that the oil can effectively lubricate the compressor.
In reality, different refrigerants have varying degrees of these desired properties making choice a matter of trade off. The change in priorities over the last century from safety to environmental protection continues to drive change in refrigerant choice.
History & regulation of refrigerants
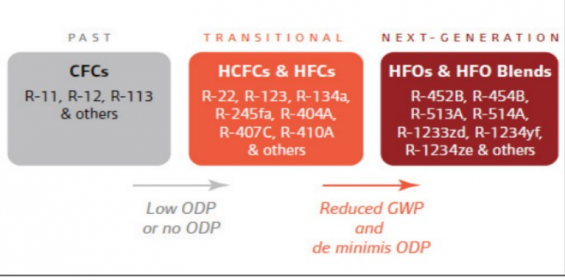
The first commercial refrigerants used toxic or flammable gases, such as ammonia, methyl chloride, or propane that could result in fatal accidents when they leaked. A non-toxic and non-flammable chlorofluorocarbon (CFC) gas was developed in 1928 (R-12) and branded Freon by DuPont later replaced by hydrochlorofluorocarbon (HCFC) commonly R-22 and hydrofluorocarbon (HFC) refrigerants. These refrigerants were frequently used for industrial purposes as they delivered a high level of safety and efficiency combined with low installation costs.
Most of these common CFC, HCFC, and HFC refrigerants are greenhouse gases that contribute to global warming and may deplete the ozone layer when leaked to the atmosphere. R-22 for example has a global warming potential (GWP) about 1,800 times higher than CO2.
Regulations have become increasingly strict with the Montreal Protocol in 1987 and the Kyoto Protocol in 1997 resulting in a shift to refrigerants with even lower environmental impact. In the UK, regulations came into force in 2002 banning the use of ozone-depleting HCFC refrigerants such as R-22 in new systems. Legacy chillers that use this refrigerant however can still be serviced and maintained.
EU F-gas regulations came into force in 2015 to reduce emissions of fluorinated greenhouse gases (F Gases) through phasedown quotas, bans and maintenance requirements.
Limiting the amount of F-gases sold in the EU from 2015 phasing down in steps to one-fifth of 2014 sales in 2030.
Banning F-gases in many new types of equipment
Preventing emissions of F-gases from existing equipment by requiring checks, servicing and recovery of the gases at the end of the equipment’s life
These regulations and market demand for more environmentally friendly solutions has driven much innovation in industrial process and HVAC temperature control with many new refrigerants such as R-454b and R513a being adopted.
Refrigerant safety classifications
Refrigerants are categorised according to toxicity and flammability. There are two classes for toxicity; lower toxicity (Class A) where toxic concentrations are less than or equal to 400 parts per million (PPM) by volume and higher toxicity (Class B).
There are four classes of flammability: 1, 2L, 2 or 3. Class 1 is for refrigerants that show no flame propagation at 140°F (60°C) ranging to class 3 highly flammable. The purpose of the 2L subclass is to reflect the lower flammability properties of the new low-GWP refrigerants, such as hydrofluoro-Olefins (HFOs), like R-1234yf and R-1234ze.
Ozone Depletion Potential (ODP) and Global Warming Potential (GWP)
All refrigerants have an Ozone Depletion Potential (ODP) and Global Warming Potential (GWP) rating. The Ozone Depletion Potential (ODP) is the relative amount of degradation to the ozone relative to R-11 (or CFC-11) being fixed at an ODP of 1.0. It is the ratio of global loss of ozone to the global loss of ozone from CFC-11 of the same mass.
Hydrochlorofluorocarbons have ODPs mostly in range 0.005 - 0.2 due to the presence of the hydrogen which causes them to react readily in the troposphere, therefore reducing their chance to reach the stratosphere where the ozone layer is present. Hydrofluorocarbons (HFC) have no chlorine content, so their ODP is essentially zero.
Global Warming Potential (GWP) is the heat absorbed by any greenhouse gas in the atmosphere, as a multiple of the heat that would be absorbed by the same mass of carbon dioxide (CO2). GWP is a measure of how environmentally detrimental refrigerants can be relative to C02 which has a GWP of 1.0
New low GWP refrigerants
While the EU market was 71% R-410a for new equipment sold in 2020, new lower GWP refrigerants such as R-454b are poised to take over from 2021.R-454b is an HFO (Hydro Olefin) refrigerant made by blending the single component R-32 refrigerant with R-1234yf giving some unique advantages. R-32 on its own has a high discharge temperature which can limit its operating envelope without some type of injection. R-454b however is an easier refrigerant to handle and offers similar properties to R-410a, making it a cost-effective & easy to use solution in new equipment without major modifications being necessary, ideal for industrial process applications. R-454b also has a lower GWP of 466 compared to R-32 at 675 and has an ozone depletion potential (ODP) of zero.
Operating pressure requirement of new refrigerants
While the next generation of refrigerants balance the needs of safety and reduction in carbon footprint, the new trade off is the development and cost of the equipment to cope with the increased pressures required for these refrigerants to work. As a direct replacement for R-410A, R-454B operates at a slightly lower pressure where as R-32 requires a slightly higher pressure. Next generation refrigerants deliver improvements in the coefficient of performance (COP), the ratio of useful heating or cooling provided to work required or energy usage of the compressor. This comes with a slight flammability trade-off having some implications on chiller placement and maximum charge (hence capacity). It also means components need to be compatible with flammable refrigerants, to ensure they can’t be considered an ignition source.
*Richard Payne is marketing director at ICS Cool Energy Group
https://twitter.com/icscoolenergy
https://www.linkedin.com/company/ics-temperature-control/
https://www.facebook.com/icscoolenergy/